Eğer lisede cebir dersi gördüyseniz (veya şimdi öğreniyorsanız), muhtemelen ikinci dereceden denklem formülünü tanırsınız. Eğer tanımadıysanız, beyniniz muhtemelen onu baskılamıştır.
Bu noktada milyarca kişi, ikinci dereceden denklemleri çözmek için bu ağır denklemi öğrenmek, hatırlamak ve uygulamak zorunda kalıyor. Ancak Carnegie Mellon Üniversitesi’nden matematikçi Po-Shen Loh’a göre, aslında en başından beri daha kolay bir yol varmış ancak binlerce yıl boyunca gizli kalmış.
Loh, yayınladığı yeni bir araştırma makalesinde bu formülü tebrik ediyor ve formülün, MÖ 2000 civarındaki Eski Babil Dönemi’nin başlangıcına dek uzanan, “ilk matematikçilerin büyük başarısı” olduğunu söylüyor. Fakat formülün bazı antik kusurlarını da rahatça kabul ediyor.
“Bu formülün aynı zamanda, milyarlarca insanın hatırlamak zorunda kaldığı ve çok karmaşık olan ilk (belki de tek) formül olması üzücü” diye yazıyor Loh.
Matematik öğrenenlerin dört bin yıldır yerine getirdiği bu ağır görev, belki de aslında çok gerekli değildi. İkinci dereceden denklem formülünün, elbette çarpanlara ayırma, tam kareye tamamlama ve hatta grafik çıkarma gibi alternatifleri her zaman vardı. Fakat bu formül; biraz anlaşılmaz olsa da, ikinci dereceden denklemleri çözmede genelde en kapsamlı ve güvenilir yöntem olarak düşünülüyor. Formül şöyle görünüyor:
Bu formül, ax2 + bx + c = 0 olan standart denklemleri çözmede kullanılıyor.
Loh, Eylül ayında ikinci dereceden denklemlerin ardındaki matematik üzerinde beyin fırtınası yaparken; aynı formülün yeni ve basit bir şekilde türetilebildiğini keşfetmiş. Bu alternatif yöntem, Loh’un makalesinde belirttiği üzere; “İkinci dereceden genel denklemleri çözme konusunda hesaplama bakımından verimli, doğal ve hatırlaması kolay bir algoritma.”
Loh, keşiften bahsederken “şaşkınlıktan dilinin tutulduğunu” söylüyor. “Bunu nasıl daha önce hiç görmemiş olurum? Hiçbir ders kitabında görmemiştim.”
Loh’un bu yeni yönteminde, ax2 + bx + c = 0 denklemindeki b‘yi oluşturan iki rakamın toplamına yoğunlaşan bir ortalama tekniği kullanılıyor. Fakat genelde öğretilen yöntemde, c‘yi oluşturan iki rakamın sonucuna odaklanılıyor ve problemlerin çözülmesi için sıklıkla tahmin yapılması gerekiyor.
“Bu yüzden, eğer iki rakamın toplamı 2 ise, o halde ortalamaları 1’dir” diye açıklıyor Loh internet sitesinde.
“Bu yüzden rakamlar ne olursa olsun, aynı miktarın 1 fazlası ve 1 eksiğidirler. Tek yapmamız gereken, 1+z ve 1-z‘nin iki rakam şeklinde işleyeceği bir z bulmak. z sıfır da olabilir.”
Bu z değeri, Loh’un alternatif iki bilinmeyenli denklem yöntemiyle belirlendiğinde, diğer bazı koşulların sağlanması şartıyla tüm ikinci dereceden denklemlerin kökleri çözülebiliyor.
Loh makalesinde, “konunun 4.000 yıllık tarihi göz önüne alındığında; bu yaklaşım bugüne kadar tümden gözden kaçtıysa çok şaşıracağını” söylüyor ancak (Babilli, Yunan ve Fransız matematikçilerin önayak olduğu adımları bir araya getiren) bu alternatif yöntemin “kesinlikle yaygın biçimde öğretilmediğini veya bilinmediğini” belirtiyor. (Yazar, İngilizce kaynaklarda buna dair bir bulguya rastlamamış.)
MATEMATİK DERS KİTAPLARI TARİHİ EŞİKTE OLABİLİR
Ancak; bu basit kanıtı tanımlayan ön baskı makalesini Ekim ayında ilk kez internette paylaştıktan sonra, dikkatinin 1989 tarihli bir araştırma makalesine gittiğini ve makalenin, bu yöntemin bilfiil aynısı olduğunu söylüyor. Böylelikle, bu alternatif yöntemin daha önce tanımlanmamış olduğuna yönelik kuşkusunu gerekçelendirmede biraz yol kat etmiş.
O halde çözülmesi gereken tek şey, bu yöntemin neden daha önce yaygın şekilde bilinir hale gelmemiş olduğu. Çünkü Loh’un deyimiyle bu yöntem, “İki bilinmeyenli denklemlerin çözümünde, ana müfredata eklenmesi bakımında faydalı olabilecek güzel bir alternatif yaklaşım sunuyor.”
(Tabi böylelikle, bir daha kimse iki bilinmeyenli denklem formülünü hatırlamaya ihtiyaç duymayabilir.)
Bu yöntemin binlerce yıl boyunca nasıl bu kadar dikkatten kaçtığını hâlâ bilmiyoruz fakat eğer Loh’un sezgileri doğruysa, matematik ders kitapları tarihi bir eşiğin kıyısında olabilir; ayrıca, ders kitaplarını değiştiren keşifleri hafife almayın.
“Bunu mümkün olduğu kadar fazla şekilde dünyayla paylaşmak istedim” diyor Loh. “Çünkü bu yöntem, pek çok insana matematiğin belki de kendileri için olmadığını düşündüren karmaşık bir bölümünün gizemini ortadan kaldırabilir.”
Araştırma makalesi, ön baskı sitesi olan arXiv.org‘da bulunabilir. Po-Shen Loh’un bu basit kanıta yönelik genel açıklamasını ise buradan okuyabilirsiniz.
Yazar: Peter Dockrill/ScienceAlert. Çeviri: Ozan Zaloğlu.
Matematikçiler, Yapay Zeka’nın Asla Çözemeyeceği Bir Hesaplama Problemi Geliştirdi


![012-quadratic-equations_1024[1]](https://popsci.com.tr/wp-content/uploads/2019/12/012-quadratic-equations_10241.jpg)
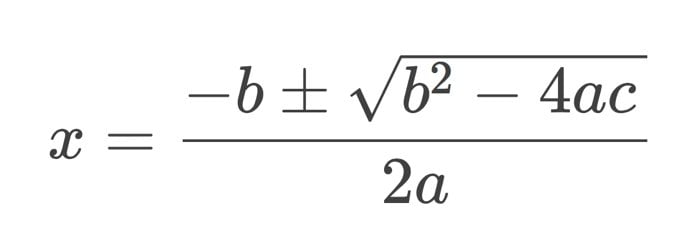



Zaten 11.sınıf matematik müfredatında bu formül mevcut ve yıllardır kullanılıyor.
Onların müfredatında yokmuş onlar hiç görmemiş. O açıdan bak olaya
( Carnegie Mellon Üniversitesi’nden matematikçi Po-Shen Loh) bak adam üniversitede matamatikci hiç görmemiş. Biz 11. Sınıf müfredatında yıllardır okutuyoruz. Çılgın Türkler diye boşa dememişler. Eğitimde ne kadar ilerdeyiz anlayalım
komik bir durum :D Adamlar formulü illa garantiye alacaklar diye (herhalde) Kullanmamışlar :D :D
Yalnız gençler burada yeni çıkan formül verilmemiş. Eskisinden bahsediliyor dikriminat tan haberiniz olsun
Formülü anladım. X2+2x-2=0 denkleminin reel kökü yok.kokler toplamı -2 olduğundan köklerin reel kısmı -1olur. Kökler çarpımı (-1+koka/2)(-1-koka/2)=1-a/4=-2 ise a=12 olur.