Antik Mısır Matematikçileri: İsimsiz Kahramanlar

(MÖ 2000 civarı) Yine tarih öncesi döneme uzanıyoruz. Bu sefer matematiğin ilk ortaya çıktığı yerde; Nil havzasındayız, yani Antik Mısır uygarlığında.

İnsanlık, tarih boyunca üzerinde yürüdüğü gezegeni ve üstünü örten gökleri anlamaya çalıştı. Dünyanın temel işleyişini çözmek, çevremizdeki nesnelerin özelliklerini ve bunları belirleyen kuralları anlamak, bizimle ve birbirleriyle olan ilişkilerini keşfetmek zorundaydık.
Bu uğurda ortaya konan tüm tarih öncesi çabalar, doğanın kendisine özgü bir düzeni olduğunu ortaya çıkardı. Bu kapsamlı düzen matematikti.

Doğa sürekli değişir. En ilkel toplumların bile rahatça fark edebileceği bu değişimleri izlemek büyük bir mesele değildi. Gündüz geceye döner, mevsimler değişir, bitki ve hayvanlar bu değişimlere ayak uydurur. Yani doğa bazı kalıpları tekrar eder. Peki bu kalıplar ve dönüşümlerin bir anlamı var mıydı?

Büyük ihtimalle matematiğin keşfine gidilen yolu bu soruya aranan yanıt aydınlattı. İngiliz matematikçi Marcus du Sautoy, “Matematiğin en önemli kavramları, yer ve miktar, fiziksel olarak beynimize işlenmiştir” diyor. Hayvanların bile sayı ve mesafe algıları olduğunu
biliyoruz. Bunu öğrenmiyorlar; doğuştan “biliyorlar”. Bizler de öyle…

Beynimiz matematik kullanımına uygun gelişmiş. Ne de olsa ilkel toplumlar için, matematiği anlamak, ölüm kalım meselesine dönüşebiliyordu. Bir noktada saymaya, kuralları anlamaya, ilişkileri çözüp yakın çevremizdeki dünyayı düzenlemeye de başladık. Ancak Nil nehri kıyılarında yaşayan Mısırlılar onu bambaşka şekillerde kullanmayı da öğrendi.

Mısır tarımı, Nil nehrinin taşmasıyla gerçekleşiyordu. Bu sebeple Nil’in taşmasını yeni bir yılın başlangıcı olarak kabul ettiler. Zamanı ölçmeye başlayan Mısırlılar belirli zaman aralıklarında yaşanan değişimleri de kayda geçiriyordu. Örneğin Ay’ın evrelerini ve iki evre arasında geçen süreyi biliyorlardı.

Antik Mısır uygarlığı hızla gelişip büyüdü ve böylece düzeni oturtacak yeni yöntemlere ihtiyaç duyuldu. Örneğin artık tarım topraklarının kapladığı alanı, ürün miktarını hesaplamaları gerekecekti. Vergiler de düzenli olarak toplanmalıydı. Bu sırada ölçüm yapmak için vücutlarını kullandılar. Bir el genişliği ölçüsü (palm) ve dirsekten parmak
uçlarına olan mesafe (cubit) gibi standartları vardı. İkincisini daha büyük ölçekli alanlara da uygulayabildiler. Tarım alanlarını da aynı şekilde ölçtüler. Hatta firavunlar bu ölçümlerin sürekli yapılmasını emretmiş olmalı. Ne de olsa değişimler de sürekliydi. Ancak bu hesaplamaları kayıt altına almak için de bir yöntem bulmaları gerekiyordu. İki elde toplam 10 parmak olduğu için onluk sistemi kullandılar; 1 rakamı için düz bir çizgi, 10 için at nalı,
100 için çengel, 1000 içinse lotus çiçeği sembolleri kullanıldı.

Mısır sayı sisteminde basamak değeri kavramı bulunmuyordu. Böyle büyük bir sayıya hiç ihtiyaç duydular mı, bilinmez. Ama örneğin 1.000.000 yazabilmek için 9 düz çizgi, 9 at nalı, 9 çengel diye devam ederek toplamda 54 karakter çizmek zorunda kalmaları gerekirdi.

Mısırlıların problem çözme konusundaki başarılarını ve önemli matematiksel buluşlara imza attıklarını, papirüslere kaydettikleri için biliyoruz. Mısır papirüsleri sazlıklardan üretilirdi.
Böyle bir malzemenin binlerce yıl dayanması mucize olur. Dolayısıyla günümüze dek ulaşmayı başaran çok az sayıda papirüs mevcut. Bunlardan biri, Rhind papirüsü. İki büyük sayının nasıl çarpıldığını gösteren bu belge, Mısırlıların, Alman matematikçi Gottfried Leibniz’in binlerce yıl sonra keşfedeceği ikili sistemi kullandıklarını gösteriyor. Diğer bir deyişle; bilgisayarlar ve günümüz teknolojisinin temel dayanağı olan, 1’lerden ve 0’lardan oluşan ikili sayı sistemini keşfetmişler.

Bu papirüs M.Ö. 1650’de yazıldı. Öyle görünüyor ki amacı da gündelik sorunlara çözüm aramakmış. Örneğin en büyük sorunlardan biri, ekmek ve biranın paylaştırılmasıydı. Sadece yemek ve içeceğe para harcayan Mısırlı işçiler, 10 kişiye 9 somun ekmeğin paylaştırılması
gibi içinden çıkılamaz durumlarda haklarını eşit olarak almak istiyorlardı. Şöyle bir yöntem geliştirmişler: 9 ekmeğin 4 tanesini al ve 3 eşit parçaya böl. Bunların her biri 1/15’lik parçalar olur. Böylece herkese bir yarım, bir tane 1/3’lük, bir de 1/15’lik ekmek verilebilir.
İlk başta zor gibi görünen bu yöntem aslında oldukça pratik. Ve kesirli sayıları da bildiklerini gösteriyor. Bunun en eski kayıtlarından biri hiyerogliflerde saklı; Horus’un Gözü.

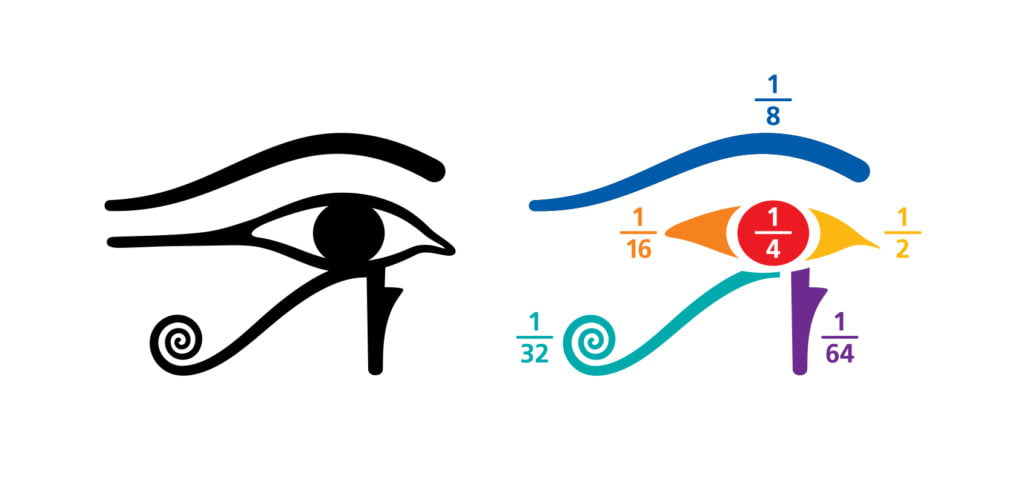
Mitolojiye göre Horus efsanesi şöyle gelişir; Horus’un babası Osiris, kardeşi Seth tarafından öldürülünce, şahin başlı tanrı Horus babasının intikamını almaya karar veriyor. Seth, Horus’la savaşırken gözünü çıkarır. Tanrılar Horus’un yanında yer aldıklarından, dağılmış
olan gözü tekrar birleştirirler. Bu gözün her bir bölümü farklı bir kesire karşılık geliyor. “Glif” denilen parçaların her biri, bir öncekinin yarısına eşit. Toplamlarıysa 63/64 ediyor. Yani tekrar bir araya getirilen göz, öncekine oranla 1/64 oranında eksik. “Sonuçta toplamı
1’e ulaşmıyor. Ancak bu eksiklik bir hata değil; anlatmaya çalıştıkları şeyi böyle
ifade etmişler.

Rhind papirüsü, Mısırlıların dairenin alanını da hesapladıklarını gösteriyor. Yöntemi nasıl geliştirdikleri bilinmiyor ancak çapı 9 birim olan dairenin alanıyla, bir kenarı 8 birim olan karenin alanının birbirine çok yakın olduğunu kayda geçirmişler. Piramitlerin mimarları simetriye dikkat ediyordu. Hatta altın oranı da bildikleri görülüyor. Altın oran, Pisalı Leonardo; nam-ı diğer Leonardo Fibonacci tarafından 1-1-2-3-5-8-13-21-34-55-89-144 şeklinde dizilenmişti. Her bir sayı, kendisinden öncekine bölündüğünde birbirine çok yakın sayılar elde edilir ama 13. sıradaki 144’den itibaren gelen tüm sayılar, bir öncekine bölündüğünde bu oran sabitlenip 1,618 oluyor. Fibonacci’nin yaptığı şey, doğada var olan güzellik oranını matematiksel olarak tanımlamaktı. Mısırlılarsa piramitlerde uygularken, iki
kenarın altın orana uygun olması için, uzun kenarla kısa kenar arasındaki ilişkiyi, iki uzunluğunun toplamının uzun kenarla olan ilişkisiyle kıyaslamışlar.

Sanatçıların, mimarların tasarımlarında ve doğada hemen her yerde görülebilen bu orandan haberdarlar mıydı, yoksa göze hoş göründüğü için içgüdüsel olarak mı uyguladılar? Bunun cevabını bilmiyoruz. Görsel ya da işitsel olarak altın oranı yansıtan her bir eser estetik açıdan güzel bulunma özelliğine sahip. Bunun en iyi örneklerine, aynı zamanda bir matematikçi olan Leonardo da Vinci’nin eserlerinde rastlamak mümkün.

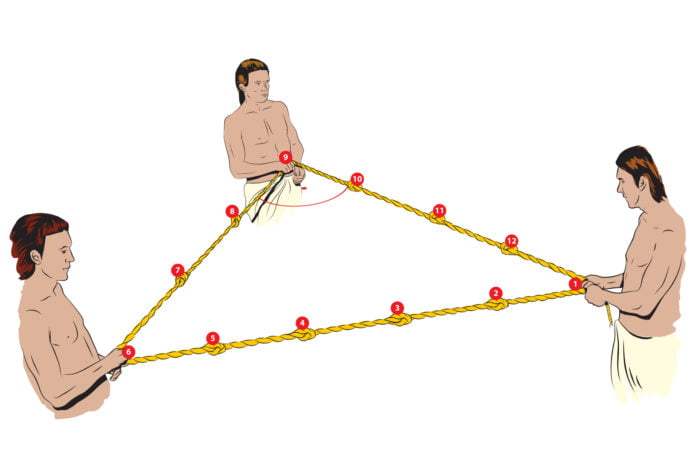
Piramitlerde uygulanmış olan bir diğer formül de Pisagor’un teoremi. Mükemmel diklik ve keskin köşeler elde etmek için düğümlü ipleri kullanıyorlardı. Sırasıyla 3, 4, 5 düğüm atılan bir ip kullanınca tam bir dik üçgen elde edeceklerini fark etmişler. Yani Pisagor üçgenini kullanmışlar. “Pisagor tüm dik üçgenlerin benzer özelliklere sahip olduğunu keşfedene dek neredeyse 2000 yıl geçmesi gerekecekti.”

Ve son olarak Moskova papirüsü olarak bilinen 4000 yıllık belgede, parçalardan bütüne ulaştıkları bir hacim hesaplama yöntemi kullandıkları da görüldü. Bu son derece şaşırtıcı ama günümüzde mühendislik ve fen fakültelerinde öğretilen kalkülüse de çok yaklaşmışlar!

Hazırlayan: Güneş Ulukuş.