Zeka ve zekanın gelişimi ile ilgili bir çok araştırma yapılmakta, gerek eğitim dünyasının gerekse ailelerin göndeminde sürekli olarak bu kavramlar güncel yerini korumaktadır.
Her ne kadar aşırı önem verildiğini düşünsem de zekânın ölçülmesinde kullanılan ölçekler göz önüne alındığında, çoğunda görsel, işlemsel akıl yürütme temelli matematik-aritmetik tabanlı sorular olduğunu görebiliriz. Matematik, çocuklarda ve kendi yaşamımızda çoğu zaman en çok geliştirmek istediğimiz becerilerin başında geliyor. Hiç eğitim almamış, ya da oldukça az eğitim almış bir zihnin saf matematik zekâsı ile üst düzey matematik problemlerini çözmesi, yeni teoremler geliştirmesi hatta dünyanın en ünlü matematikçilerinden biri olması mümkün mü, yoksa eğitim olmadan bu mümkün değil mi?
Srinivasa, 1887 yılında Hindistan’ın Erode kentinde ve ekonomik olarak oldukça kötü bir ailenin çocuğu olarak dünyaya geldi. Erken yaşlarından itibaren matematikte inanılmaz beceriler göstermeye başladı. Gerçekleştirdiği işlemler ve hızlıca öğrenmesi, öğretmenlerini çok şaşırtıyordu. Özellikle 10-11 yaşlarında iken bu başarısı sınıfındaki diğer arkadaşlarıyla da ilişkilerini kötü anlamda etkiliyordu. Onlarla aynı dili konuşamadığını çok geç olmadan fark etti, çünkü matematik ve düşünme derinliği açısından aralarında ciddi farklar vardı. 13 yaşında hayatının en önemli kitaplarından biri olan İleri Trigonometri kitabı ile karşılaştı. Kitap sayesinde o kadar çok derinleşti ki, gerçekleştirdiği işlemleri öğretmenleri bile takip edemiyor çoğu zaman anlayamıyordu. Srinivasa, adeta bambaşka bir seviyede ve derinlikte matematik ve düşünme evreninde yaşıyordu.
Sadece matematik yapmak istiyordu
Ekonomik olarak çok kötü durumda olması, iyi okullarda eğitim almasını engellese de matematikte ki üstün başarısı ile, Srinivasa, lisede Rangonatta Rao matematik ödülünü kazandı ve bu ödülle birlikte ülkenin önemli üniversitelerinden biri olan Government Art College’da tam burslu öğrenci olma imkanını yakaladı. Bu onun için hayati açıdan önemliydi zira açlık sınırında bir yaşam sürüyordu ve bu okulda mevcut ekonomik imkanlarıyla okuması mümkün değildi. Srinivasa’nın tek derdi matematik çalışmaktı, saatlerce, günlerce başından kalkmadığı oluyordu. Bunun yanında diğer dersleri hiç önemsemiyor, derslere gitmiyor sınavlarına bile girmiyordu. Matematikte tam puan alarak dönemi bitirse de diğer derslerin çoğundan kaldı ve bursunu da kaybetti. Ekonomik sebeplerden başka bir okulda da okuma şansı yoktu. Tam bir hayal kırıklığıydı, aslında çok çalışıyordu ama sadece öğrenmek istediği alanla, yani sadece matematik yapmakla uğraşıyordu. Kendisine bir fırsat daha sağlamak amacıyla, sınavla öğrenci alan Pachaiyappa College’a başvuruda bulundu ve sadece matematik sorularını yaptı. Matematik sorularında tam puan alarak ikinci bir okul deneyimine hak kazandı. Ancak yine aynı şey oldu. Diğer derslere olan ilgisizliği onu matematikte derinleşme fırsatından alıkoydu ve yine bursunu kaybetti, okuldan ayrıldı.
Bir muhasebecide aylık 20 rupiye bir iş buldu, karnını bile doyuramadığı yaşamına yokluk içerisinde devam etti. Gündüzleri muhasebe işlerinde çalışıyor, geceleri ise durmaksızın matematik yapma peşinde koşuyordu. Kendisine hiç iyi bakmıyor, az yiyor hatta hiç yemek yemiyordu. Aynı tür ve yetersiz beslenme, hastalıklara karşı onu çok güçsüz kılıyor, ama yine de aynı şekilde yaşamaya devam ediyordu. Hindistan Matematik Topluluğu kurucusu Aiyer ile tanışması onun için bir dönüm noktası oldu. Çalışmalarını defterlere yazan Srinivasa Ramanujan, her ne kadar formal bir matematik eğitimi almasa da inanılmaz denklemler ve teoremler bulmuştu. Onun notlarını ilk kez gördüğünde Aiyer’in tepkisi “Çarpıldım!” demek olmuştur. Aiyer, alanda tanınmış olduğundan liderlik ederek Ramanujan’ın elinden tutmuş, zamanın Hindistan Matematik Topluluğu başkanı Rao ile tanıştırmıştır. Rao, gördüğü çalışmaları Ramanujan’ın yaptığına inanmadı, çünkü bu mümkün değildi. Bu kadar eğitimsiz birinin eşi benzeri görülmemiş bu teoremleri bulmuş olması imkansızdı. Onunla özel görüşmeler ve çalışmalarından kesitler dinleyen Rao, sonunda ikna oldu ve Madras Üniversitesi’nde Ramanujan’a araştırmacı olarak matematikte çalışması adına bir fırsat daha sundu.

Dehanın keşfi
Muhasebeci olarak çalışmasına da devam eden Ramanujan için, patronlarından birinin çalışmalarını devrin ünlü matematikçilerine posta yoluyla yollaması her şeyi değiştirdi. Zamanın ünlü matematikçisi G.H. Hardy’e ulaşan yazıda geçenler başta Hardy için bir tür dolandırıcılık gibi geldi. Ancak metinleri okudukça gözlerine inanamadı. Mektup içerisindeki notları bir matematikçi yazmış olamazdı çünkü ispatlarda izlenen sıra izlenmemişti ancak matematiksel ifadelerle dolu 9 sayfanın 3. sayfasında yer alan bir tanesi, henüz bilinmeyen inanılmaz bir denklemdi. Hatta öylesine iyiydi ki matematiğin kralı olarak bilinen Gauss’un çalışmasından bile ötedeydi. Bunu matematiksel ispat yazmayı bilmeyen biri yazmıştı ama kesinlikle bir dâhiydi. Bu, Ramanujan için gayet normaldi çünkü hiçbir zaman formal bir matematik eğitimi almadı doğal olarak üst düzey bir matematiksel ispat nasıl yapılır bilmiyordu. Doğal olarak aldığı notlar ve çalışmaları kopuk kopuk görünüyordu.
Hardy, Ramanujan’ın mektubuna hemen bir cevap yazdı şöyle başlıyordu: “Sayın Ramanujan, mektubunuz ve teoremleriniz ile oldukça ilgilendim…” Uzun uzadıya yazılan mektupta kendisine gönderdiği teoremlerle ilgili görüşlerini bildirdi. Ardından Ramanujan’ı devrin en önemli matematik çalışmalarının yapıldığı Cambridge Üniversitesi’ne davet ederek önemli bir yol açtı. Hardy ve Ramanujan, 5 yıl boyunca Cambridge’te, birbirlerine karakter, dünya görüşü v.b. her anlamda ters olan iki insan, tek ortak noktaları olan matematik alanında tarihe damga vuracak çalışmalar gerçekleştirdiler. Doktora çalışmasını 1916 yılında tamamlayan Ramanujan, çalışmasının bir kısmının yayımlanması ile inanılmaz bir üne kavuştu. Sonsuzluk ve sonsuz içeren hesaplamalarda tam bir deha olan Ramanujan, 300’e yakın teorem ispatladı ve buluşları her biri diğerinden çok daha önemli olarak birçok bilim alanında karşımıza çıktı. Ramanujan’ın hayat tarzı ve yemek ile ilgili sıkıntıları İngiltere’de onu çok zorladı, yetersiz beslenme yüzünden sağlığını neredeyse kaybeden Ramanujan, 1919 yılında Hindistan’a döndü ve 1920 yılında henüz 34 yaşındayken hayatını kaybetti.
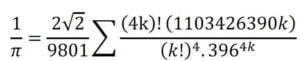
100 yılda değişen ne oldu?
Srinivasa’nın başından geçen eğitimsel olaylar günümüzden yaklaşık 100 yıl önce gerçekleşti, ancak aynı davranışa hala birçok yetenekli çocuğun maruz kaldığını görmekteyiz. Üstün yetenekli, üstün zekâlı veya dâhi bireylerin çoğu zaman çevrede yalnızlaştığını, akranları tarafından dışlandığını, beceri ve isteklerine göre eğitim alamadıklarını ve rastgele yönlendirmelerle belki bir başarı yakaladıklarını sıkça görmekteyiz. Bu durumun eğitim sistemimiz açısından gelişmesi, sayıları azımsanmayacak ölçüde olan bu bireyler için hayati bir önem taşımakta. Üstün yetenekli, üstün zekâlı ya da dâhi bireylerin derinleşmek istedikleri alan yerine, onlara neredeyse hiç faydası olmayacak birçok dersi aldıklarını ve zamanlarını onlara göre hatta bana göre de çoğu zaman faydasız geçirdiklerini görmekteyiz. Bireylerin erken dönemden itibaren beceri ve yetenekleri doğrultusunda yönlendirilmesi, becerilerine göre bir bireysel program oluşturulması çok önemli. Bu anlamda rehbersiz kalan binlerce öğrencimizin doğru yönlendirilmemesi, onları yaşam başarısı yüksek olabilecek bir hayattan maalesef uzak tutuyor.

Hayatın dönüm noktaları
Başka bir nokta olarak, potansiyeli yüksek, üstün yetenekli, üstün zekâlı ya da dâhi düzeyinde bireylerin, erken yaşlardan itibaren onları etkileyecek, motive edecek ve yönlendirecek materyal, kitap, dergi ve kişilerle tanışması her zaman çok önemli. Ramanujan için, hayatın dört dönüm noktasından oluştuğunu görmekteyiz. İlki 13 yaşında karşılaştığı İleri Trigonometri, ikincisi 16 yaşında 5000 teoremin içinde bulunduğu ama bu teoremlerin çoğunun ispatı olmayan Elementary Results in Pure and Applied Mathematics kitapları. Bu kitapların içerisinde adeta kaybolan Ramanujan, “sonsuz” kavramının derinliklerini bu kitaplar sayesinde keşfetmiştir. Üçüncü olarak Hindistan Matematik Topluluğu başkanı Rao ve tabii ki her zaman yakın arkadaşı ve bu dehayı bize kazandıran kişi olan G. H. Hardy ile tanışması. Bu anlamda potansiyel yetenekli bireylere kendilerini bulacakları fırsatları vermek hem kendilerine hem de toplumun her kesimine karşı yapılacak en büyük fayda olarak görülebilir. Çok merak edenler için Ramanujan’ın hayatını anlatan “Sonsuzluk Teorisi” filmini ve G. H. Hardy’nin Türkçe olarak yayımlanan kitabı “Bir Matematikçinin Savunması”’nı öneririm. Doğum tarihi 24 Aralık olan, hayatın her zorluğuna karşı çalışmayı asla bırakmayan Ramanujan’a saygıyla… Matematik yapmakla ve sevgiyle kalın.
Dr. Burak Karabey, Dokuz Eylül Üniversitesi, Üstün/Özel Yetenekliler Eğitimi Anabilim Dalı





